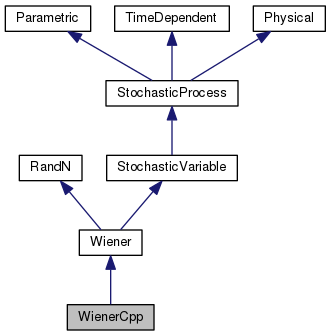
Condensed Poisson Process. More...
Public Member Functions | |
| WienerCpp (class Time *time, double w, double n, double lambda, double n_rc, double lambda_rc) | |
| Constructor. More... | |
| virtual string | getParameter (const string &p) const |
| Get parameter. More... | |
| virtual void | setParameter (const string &p, const string &d) |
| Set parameter. More... | |
| virtual void | init () |
| Initialise time-dependent values. | |
 Public Member Functions inherited from Wiener Public Member Functions inherited from Wiener | |
| virtual void | prepareNextState () |
| Calculate next value (preparing next step). More... | |
 Public Member Functions inherited from RandN Public Member Functions inherited from RandN | |
| RandN () | |
| Construct. | |
| ~RandN () | |
| Destruct. | |
| double | dRandN () |
| Retrieve random variable. More... | |
| double | dRandE () |
| Retrieve random variable. More... | |
 Public Member Functions inherited from StochasticVariable Public Member Functions inherited from StochasticVariable | |
| StochasticVariable (class Time *time, const string &name="", const string &type="Stochastic Variable") | |
| Create. | |
| double | operator() () |
| Returns the value at the current time step. More... | |
| double | d () |
| Returns the increment at the current time step. More... | |
 Public Member Functions inherited from StochasticProcess Public Member Functions inherited from StochasticProcess | |
| StochasticProcess (class Time *time, const string &name="", const string &type="Stochastic") | |
| Create. | |
| virtual | ~StochasticProcess () |
| Destroy. | |
| virtual void | proceedToNextState () |
| Proceed one time step. More... | |
| bool | isNextStatePrepared () |
| Whether. | |
| virtual double | getIncrement () |
| Returns the increment. More... | |
| virtual double | getCurrentValue () |
| Returns the value of the process. More... | |
| virtual double | getNextValue () |
| Returns the next value of the process. More... | |
| virtual void | setNextValue (double d) |
| Set the next value of the process. More... | |
| virtual void | setCurrentValue (double d) |
| Set the current value of the process. More... | |
| void | setDescription (string s) |
| Set stochastic description. | |
| string | getDescription () |
| Get the name. More... | |
 Public Member Functions inherited from Parametric Public Member Functions inherited from Parametric | |
| string | getType () const |
| Type of object. | |
| string | getName () const |
| Name of object. | |
| void | setName (const string &name) |
| Name of object. | |
| string | getConfiguration () const |
| Returns the configuration of the object. More... | |
| string | getAllParameters () const |
| String with all parameter settings. | |
| void | addParameter (const string &name) |
| Add a parameter. More... | |
| void | rmParameter (const string &name) |
| Remove a parameter. More... | |
 Public Member Functions inherited from TimeDependent Public Member Functions inherited from TimeDependent | |
| TimeDependent (class Time *time) | |
| Construct. More... | |
| virtual class Time * | getTime () const |
| Return pointer to the time object. | |
 Public Member Functions inherited from Physical Public Member Functions inherited from Physical | |
| Physical () | |
| Construct. | |
| Physical (const Physical &) | |
| Copy. | |
| Physical (string name) | |
| Construct. | |
| Physical (string name, string unitPrefix, string unitSymbol) | |
| Construct. | |
| Physical (string name, Unit unit) | |
| Construct. | |
| virtual string | getPhysicalDescription () |
| Returns the physical description. More... | |
| virtual string | getUnitName () |
| Returns the unit name. | |
| virtual string | getUnitSymbol () |
| Returns the unit name. | |
| virtual void | setPhysicalDescription (string name) |
| Set the name. Same as setDescription(). More... | |
| virtual void | setUnit (Unit u) |
| Set the unit. | |
| virtual void | setUnitPrefix (int n) |
| Set unit prefix. More... | |
| virtual Unit | getUnit () const |
| Retrieve the unit. | |
Additional Inherited Members | |
 Protected Member Functions inherited from Parametric Protected Member Functions inherited from Parametric | |
| Parametric (const string &name, const string &type) | |
| Create object of type and name. | |
| virtual | ~Parametric () |
| Destroy object. | |
 Protected Attributes inherited from StochasticProcess Protected Attributes inherited from StochasticProcess | |
| double | stochCurrentValue |
| the current value | |
| double | stochNextValue |
| the next value (direct future) | |
| bool | stochNextStateIsPrepared |
| whether prepareNextState() was successful | |
| string | stochDescription |
| the name of the quantity | |
Detailed Description
Condensed Poisson Process.
Lets assume a set of Poisson process 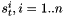 , where
, where 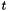 denotes time, and
denotes time, and 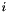 is the index of the process. Each process is multiplied by a weight
is the index of the process. Each process is multiplied by a weight  ,
, 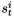 takes values of
takes values of 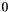 or
or 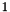 (where
(where 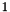 indicates an event), and events occur with a rate of
indicates an event), and events occur with a rate of 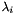 . We are interested in the sum
. We are interested in the sum
![\[s_t = \sum_i w_i s^i_t.\]](form_58.png)
Let's assume that in this collection of events coincident events happen. Coincidences are events which occur at the same time at various processes. If these events are viewed as a separate process 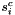 with a weight
with a weight  and a rate
and a rate 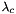 , all processes stay independent. The impact of the coincidence events depends on the sum of the weights of the processes taking part. We shall call the sum of the weights of the processes which take part the Coincidence Weight. The coincidences occur with a specific rate which we will call Coincidence Rate
, all processes stay independent. The impact of the coincidence events depends on the sum of the weights of the processes taking part. We shall call the sum of the weights of the processes which take part the Coincidence Weight. The coincidences occur with a specific rate which we will call Coincidence Rate 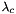 .
.
Since the events which form the coincidence event are taken out of the process 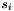 where the happened, the rate of these single processes is expected to decrease, according to the coincidence weight and the coincidence rate:
where the happened, the rate of these single processes is expected to decrease, according to the coincidence weight and the coincidence rate: 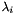 will become
will become 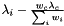 . Thus the sum of events
. Thus the sum of events 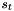 , as well as its mean
, as well as its mean 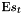 will not be affected by the correlations:
will not be affected by the correlations:
![\[ s_t = \sum_{i}w_is^i_t + w_cs^c_t. \]](form_66.png)
![\[ \mbox{E}{s_t} = \sum_i w_i\left(\lambda_i - \frac{w_c\lambda_c}{\sum_iw_i}\right) + w_c\lambda_c \]](form_67.png)
![\[ = \sum_i w_i\lambda_i \]](form_68.png)
The variance of this process 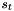 will be:
will be:
![\[\mbox{Var}\{s_t\} = \sum_i w_i^2\left(\lambda_i - \frac{w_c\lambda_c}{\sum_iw_i}\right) + w_c^2\lambda_c.\]](form_69.png)
These parameters will be used to construct a white-noise (Wiener) process, which feeds the neuron: Let's assume the neuron is connected to many synapses which each have small weights. Lets substitute the correlation weight  - since all weights are the same - by the amount
- since all weights are the same - by the amount  of synapses taking part in a coincident pulse times their weight. We will call this amount the Coincidence Width.
of synapses taking part in a coincident pulse times their weight. We will call this amount the Coincidence Width.
Since the coincidence rate 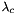 will not be higher than the overall rate
will not be higher than the overall rate 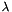 , and the coincidence width
, and the coincidence width 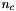 will not be higher than the overall number of synapses, it makes sense to use a relative coincidence width which ranges from
will not be higher than the overall number of synapses, it makes sense to use a relative coincidence width which ranges from 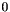 to
to 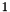
![\[ n_{rc} = \frac{n_c}{n},\]](form_76.png)
and a relative coincidence rate which ranges from 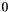 to
to 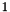
![\[\lambda_{rc} = \frac{\lambda_c}{\lambda}\]](form_77.png)
This amounts to the following expressions for mean and variance of the white-noise process:
![\[ \mu := nw\lambda \]](form_78.png)
![\[ \sigma^2 := nw^2\lambda\left(1 - n_{rc} \lambda_{rc} + nn_{rc}^2\lambda_{rc} \right) \]](form_79.png)
The condensed poisson process implements such a white-noise process.
Constructor & Destructor Documentation
| WienerCpp::WienerCpp | ( | class Time * | time, |
| double | w, | ||
| double | n, | ||
| double | lambda, | ||
| double | n_rc, | ||
| double | lambda_rc | ||
| ) |
Constructor.
- Parameters
-
time Time object w single weight n number of processes in the sum of processes lambda rate of a single process n_rc relative coincidence width lambda_rc relative coincidence height
Member Function Documentation
|
virtual |
Get parameter.
In a derived class, override this to handle every parameter you implement. If a parameter is described using multiple strings separated by space, this indicates a parameter of a parameter.
Reimplemented from Wiener.
|
virtual |
Set parameter.
Sets the value of a parameter using strings. If a parameter is described using multiple strings separated by space, this indicates a parameter of a parameter (not implemented yet).
Reimplemented from Wiener.
